統計学について

産業保健師で働く上でデータを整理したり、解析したりする必要があるかと思います。そして統計学などを色々調べることがあると思いますが、統計学を調べると、確率、変数、母集団、標本だとかでてきて余計にわからなくなることや実際どうやって使えばいいの？と思いませんか。私もそう思います。

私もまだまだ勉強中ではあり、間違えているかもしれませんが、私なりの解釈として書いていきたいと思います。

統計の考え方

統計ってどういうものかですが、たくさんあるデータをどのように整理、解釈していくか考える手法であり、そのデータを持つ意味は？そのデータをどう見るかを考えていくことかと思います。

例を挙げると・・・

このとき、皆さんはこの人は良い点を取ったと思いますか？悪い点を取ったと思いますか？

答えとしては、情報が足りないためこれだけでは判断できませんよね。

では、条件を加えると

パターン①だと平均点より高い点数を取ることがきた⇒良い結果だった

パターン②だと平均点より点数が低かった⇒悪い結果だった

（ただし中央値、ばらつき具合によってはこのようにならない場合もあります。）

データを単体で見ると、その結果が持つ意味や良し悪しの判断が難しくなります。実際の保健師の扱うデータには、健康診断の結果やストレスチェックなどのデータがあると思います。個人のデータをみただけでは、その結果が平均的なのか、平均より高い、平均より低いかわかりません。そのため、企業のデータを集計して、個人のデータを見えるようにします。また、企業の集計データが全国のデータと比較した時にどう見えるか判断していく必要があると思います。

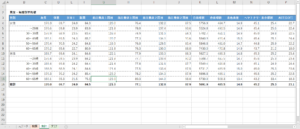
例えばですが、下記のような集計をすると男女別にさらに年齢区分でまとめています。性別や年齢によっても健康診断の結果の偏りがありますので、データを集計することによりその個人のデータがどの程度なのかわかるようになります。

（こちらはあくまでもサンプルのデータですので適当にデータに意味はありませんのでご了承ください）

使いそうな用語

働いていると呪文のように「3σがー」「3σがー」という上司がいませんか？普段働いていく中でよく聞く用語は、中央値や３σぐらいかなと思います。

平均値と中央値って何が違うの・・・と私も思っていました。

統計学を調べるといろいろ用語がでてくるかと思いますが、すべてを理解するにはかなりかなり大変だと思います。それに会社で偉そうにしている人もそこまで理解している人はいないと思います。その他にもリスク比、オッズ比などもありますが、必要があれば別の機会に説明したいと思います。最低限これらがどんな意味なのかぐらいわかっていれば集計などで特に困らないかと思います。

中央値

中央値とは、データを並べたときに中心にする値です。

例えば・・・

この貯金額を聞いて、平均的な家庭ってこんなに貯金しているの？って思う人もいるかもしれませんが、中央値はどれくらいかというと

下記のようなデータの場合に上記のような条件を満たします。つまり、データに極端に高い値、低い値がある場合に平均値はそれに引き寄せられます。中央値はあくまでもデータを順番に並べたときの真ん中のデータになります。

No.	貯金額
1	2000万円
2	1200万円
3	800万円
4	610万円
5	480万円
6	240万円
7	200万円
8	100万円
9	80万円
10	70万円
11	50万円
平均値	530万円
中央値	240万円

データによっては平均値と中央値に差があり見え方が変わってくる場合があります。そのような場合に中央値という考え方も重要となります。

3σ（3シグマ）

まずのこの「σ(シグマ)」についてですが、標準偏差になります。つまり、データのばらつきの大きさを表す指標となります。

例えば・・・

平均点60点のテストで100点満点中70点であった場合、下の2つのパターンで意味合いが変わってきますよね

No.	グループA	グループB
1	95点	74点
2	93点	70点
3	85点	62点
4	82点	60点
5	80点	60点
6	80点	58点
7	70点	58点
8	60点	56点
9	10点	56点
10	5点	54点
11	0点	52点
平均値	60点	60点
中央値	80点	58点

この記事の上の方で統計の考え方の説明をしましたが、平均値だけでは情報量が少なくそれだけでは意味がないことがあります。そのようなときにばらつきの大きさの情報が必要となってきます。

それぞれのグループの標準偏差を計算すると

	グループA	グループB
標準偏差	34.96点	6.32点

となります。（計算式などは今回は割愛させていただきます）標準偏差の値が大きくなるとばらつきが大きいとなるため、

グループAのテストでは平均より10点高くてもすごくありませんが、

グループBのテストでは平均より10点も高くてすごいとなります。

 

では、本題の3σについてですが、σの3倍における区間にデータがおさまる確率を表します。σ（標準偏差）には次のような関係があります。

1σ、2σ、3σは、それぞれσの1倍、2倍、3倍です。

3σをよく耳にたり、よく聞かれたりするのは、データがどれぐらいばらついているのか、ほとんどの人が3σ以内の数値ですよということになります。

さいごに

今回の内容はこんなこと当然知っているよという人もいると思いますが、統計や数学のように数字が並ぶと反射反応で嫌だな無理だなと思う人もいるかと思いますので、あくまで統計の取っ掛かりとして見ていただければと思います。

健康診断の結果やストレスチェックなどのデータ見やすくすることができればいいだけです！

であれば、「統計学の本読んでを一から学ぼう」と思うと挫折すると思います。

まずは仕事で使うデータをどうやってまとめたら見やすくなるかな？

この範囲で平均を取ろう！これは平均値だけではダメかな？このグラフを作ろう！

と思いつくことが大事でこれだけれも十分統計していると思います

仕事で扱うデータの集計やグラフ作成をして、もっと知りたくなった際に統計学の本を読んで知識を深めるといいと思います。

では、纏めるためにはエクセルを使ってになるかと思いますが、私ならこんな感じで集計するかな？というものも書いていきたいと思います。